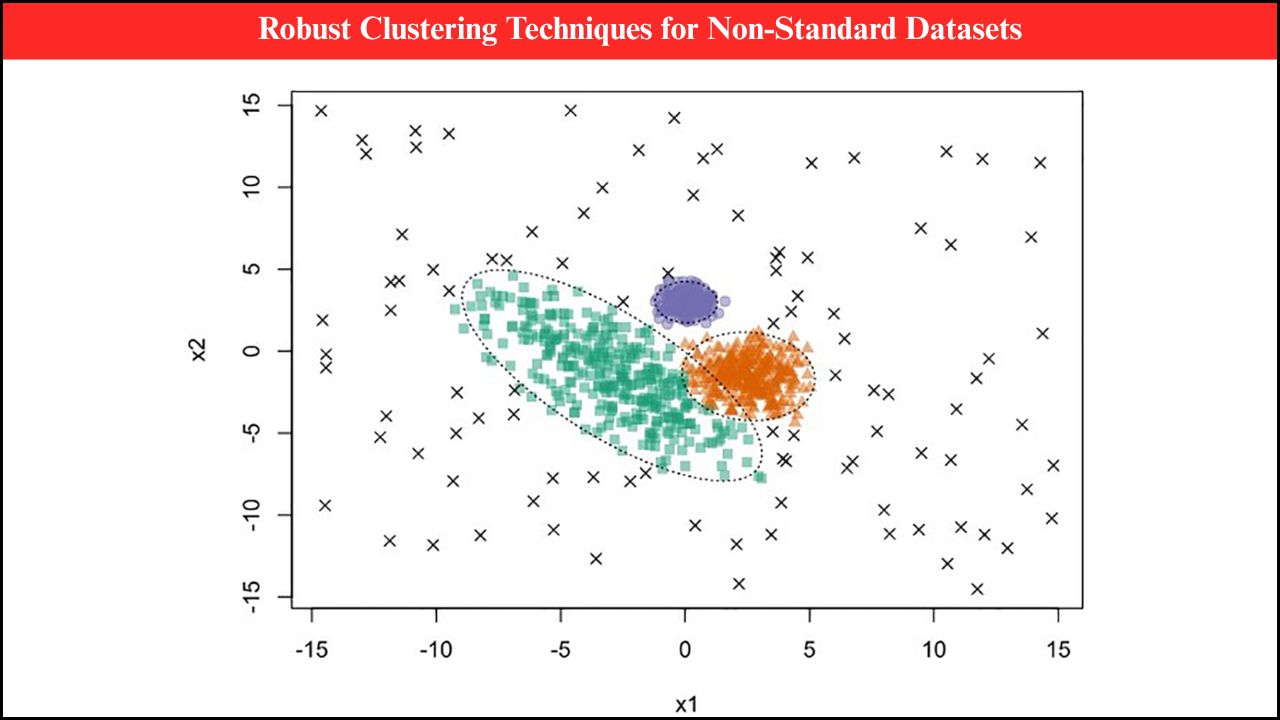
Non-parametric methods hold a significant place in modern statistical analysis because they provide flexibility in handling real-world data without the strict assumptions of parametric models. Complex data structures, such as high-dimensional datasets, irregular distributions, longitudinal observations, and mixed-type variables, often defy the assumptions of normality, homoscedasticity, or linearity. Non-parametric approaches address these challenges by adapting to the data itself rather than imposing rigid forms. This article explains the key features, applications, benefits, and limitations of non-parametric methods in the context of complex data structures.
Table of Contents
Key Characteristics of Non-Parametric Methods
- Flexibility: Methods do not assume a predefined distribution, such as normality.
- Data-driven: Techniques adapt to the structure of the observed dataset.
- Robustness: Outliers and skewed distributions have less influence compared to parametric approaches.
- Scalability: Many methods are suitable for high-dimensional or irregularly shaped datasets.
- Applicability: Useful when sample sizes are small, measurement scales are ordinal, or distributions are unknown.
Types of Complex Data Structures Addressed
- High-dimensional data – Observations with thousands of variables, such as genomic data.
- Longitudinal data – Measurements collected repeatedly over time.
- Multivariate data – Multiple correlated outcomes are analyzed simultaneously.
- Functional data – Curves, signals, or images where each observation is a function.
- Categorical or ordinal data – Data that cannot be directly analyzed with parametric models.
- Non-linear relationships – Complex dependencies that parametric regression cannot capture.
Popular Non-Parametric Techniques
- Kernel density estimation (KDE) – Estimation of probability distributions without assuming parametric forms.
- Rank-based tests – Mann–Whitney U, Kruskal–Wallis, and Wilcoxon tests for non-normal distributions.
- Nearest-neighbor methods – Classification and regression based on proximity.
- Decision trees and random forests – Non-linear and interpretable approaches for structured and unstructured data.
- Spline and smoothing methods – Flexible curve fitting for irregular patterns.
- Support vector machines (SVMs) – Non-linear classification using kernel functions.
Comparison Between Parametric and Non-Parametric Approaches
| Aspect | Parametric Methods | Non-Parametric Methods |
|---|---|---|
| Assumptions | Rely on distributional assumptions (e.g., normality) | Minimal assumptions about distribution |
| Flexibility | Limited, fixed functional forms | Highly flexible, adapts to data |
| Data Size Requirement | Efficient with small datasets | Often require larger datasets for accuracy |
| Interpretability | Coefficients have a direct meaning | Often less interpretable |
| Handling Outliers | Sensitive to extreme values | More robust to irregularities |
| Scalability | Works well for small to moderate data | Suitable for complex, high-dimensional data |
Kernel-Based Approaches for Complex Data
- Kernel density estimation provides a smooth estimate of the distribution even for multimodal datasets.
- Kernel regression helps capture non-linear trends without assuming linear relationships.
- Kernel-based clustering partitions data into groups based on similarity measures.
- Advantages include: adaptability to high-dimensional spaces and the ability to uncover hidden structures.
Rank-Based Methods for Robust Analysis
- Mann–Whitney U Test compares medians of two independent groups.
- Kruskal–Wallis Test extends rank-based comparison to multiple groups.
- The Wilcoxon Signed-Rank Test analyzes paired or matched samples.
- Strengths include resistance to non-normality and suitability for ordinal data.
- Applications are common in clinical research, psychology, and social sciences.
Non-Parametric Regression Models
- Spline regression allows flexible curve fitting across intervals.
- Local regression (LOESS/LOWESS) adapts to local neighborhoods of data points.
- Decision tree regression captures complex, hierarchical relationships.
- Random forest regression combines multiple trees for improved accuracy.
- Use cases include medical prediction, financial forecasting, and engineering analysis.
Machine Learning-Oriented Non-Parametric Methods
- K-nearest neighbors (KNN) relies on distance measures for classification and regression.
- Decision trees split data based on variable thresholds, which is useful for interpretability.
- Random forests enhance stability by combining multiple trees.
- Support vector machines (SVMs) classify non-linear data using kernel functions.
- Neural networks in their non-parametric form learn from data without explicit distributional models.
Examples of Applications
| Non-Parametric Method | Application Area | Example Use Case |
|---|---|---|
| Kernel Density Estimation | Environmental science | Estimating pollution concentration distributions |
| Mann–Whitney U Test | Healthcare | Comparing treatment effectiveness between groups |
| Random Forests | Finance | Predicting stock market movements |
| K-Nearest Neighbors | Image recognition | Classifying handwritten digits |
| Splines & LOESS | Engineering | Modeling stress-strain curves |
| SVM (Kernel) | Genomics | Classifying gene expression patterns |
Advantages of Non-Parametric Methods in Complex Data Analysis
- Adaptability to non-standard distributions and irregular patterns.
- Robustness in the presence of noise and outliers.
- Versatility across disciplines, including medicine, finance, biology, and engineering.
- Interpretability in tree-based models compared to black-box parametric models.
- Scalability to high-dimensional datasets like genomics or text mining.
Limitations of Non-Parametric Methods
- Data-intensive – Many methods require large sample sizes to achieve accuracy.
- Computational cost – Kernel-based and high-dimensional techniques can be resource-heavy.
- Less interpretability – Results may not provide clear parameter estimates.
- Overfitting risk – Flexibility sometimes captures noise instead of true patterns.
- Model selection challenges – Choosing bandwidths, kernels, or smoothing parameters requires expertise.
Advantages vs Limitations
| Aspect | Advantages | Limitations |
|---|---|---|
| Distributional Flexibility | Works without strict assumptions | May lack efficiency when parametric assumptions hold true |
| Robustness | Resistant to outliers and skewness | Can still be sensitive to extreme noise |
| High-Dimensional Data | Handles complex datasets | Computationally expensive |
| Model Interpretability | Tree-based models are intuitive | Others, like kernel methods, lack transparency |
| Accuracy | Captures non-linear structures effectively | Risk of overfitting small datasets |
Real-World Applications
- Medical research – Non-parametric survival analysis for patient lifetimes.
- Economics – Non-parametric demand estimation without rigid functional forms.
- Environmental science – Analyzing irregular climate data distributions.
- Machine learning – Developing recommender systems using neighborhood-based approaches.
- Sociology – Rank-based methods for analyzing survey responses.
- Genomics – Classifying gene expression profiles with non-parametric classifiers.
Looking Ahead
Non-parametric methods provide a powerful toolkit for analyzing complex data structures that resist conventional statistical modeling. Their strength lies in flexibility, robustness, and adaptability to data-driven patterns. While computational demands and interpretability challenges exist, the ability to uncover insights from irregular, high-dimensional, or non-linear datasets makes non-parametric techniques indispensable in modern research. A balanced approach that acknowledges both advantages and limitations ensures meaningful application across disciplines.